Puzzle
Knight's tour problem
BACKGROUND
The knight in chess is a piece which can move in an L shape. It is said to be the secret ingredient which has made chess such a popular game for so long! Allegedly, the asymmetry introduced to the board by this weird movement shape and unique property of jumping over other pieces is what makes chess such a beautiful game (all other pieces can only move straight or diagonally).
It is also the only piece that makes sense in an otherwise bizarre game. I suppose a bishop could do damage on the battlefield by being extremely judgemental, but moving a castle multiple times is impractical to say the least - good luck getting planning permission with no objections at the local council meeting multiple times. Who came up with this insane army setup?

KNIGHT'S TOUR PUZZLE
The original knight’s tour puzzle involves the Knight being placed in the top corner of the board, and goes around the board on a ‘tour’. This involves the knight jumping around on the board, and not revisiting the same square twice.

According to the Knight’s tour Wikipedia page, the puzzle has been around for a while (back to the 9th century!) with some OG mathematicians like Euler having a go at it. There are a few variations on it (different board sizes, etc) but the original 8 x 8 board has exactly 26,534,728,821,064 directed closed tours (closed meaning the Knight’s final position means for its next move it can return to the same square it started so can start the tour all over again if visiting each square once wasn’t thrilling enough for it). If you count the open tours (finishing in any old spot) the number of solutions goes up to 19,591,828,170,979,904. As you can see, it is a large number and also explains why my laptop nearly melted trying to solve it prior to using optimising heuristics.
SOLVING THE ORIGINAL KNIGHT'S TOUR
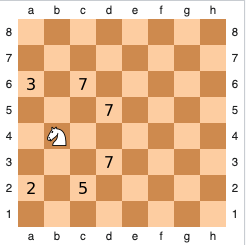
There are a few ways to solve the original puzzle. The one I looked at used a heuristic named Warnsdorff’s rule, which optimises the brute force style recursion algorithm down to linear time by defaulting to taking the move where the knight has the fewest possible options for the subsequent move. Programatically you can represent the board as a graph and sort the nodes based on the number of possible next moves. This causes the path to default to going along the edges of the board, working inwards, which supposedly saves your computer the pain of going through the dead variations where it gets stuck and can’t find a way to visit an edge square (note in the gif above showing a complete tour the pattern ends up like a thorny crown). Another way to get it down to linear time is using a divide and conquer algorithm to cut up the board and patch up the sections after completing tours on the smaller pieces.
Here is a solution from the website Geeksforgeeks in C++ that does it blazingly fast in linear time:
| // C++ program to for Kinight's tour problem using | |
| // Warnsdorff's algorithm | |
| #include <bits/stdc++.h> | |
| #define N 8 | |
| // Move pattern on basis of the change of | |
| // x coordinates and y coordinates respectively | |
| static int cx[N] = {1,1,2,2,-1,-1,-2,-2}; | |
| static int cy[N] = {2,-2,1,-1,2,-2,1,-1}; | |
| // function restricts the knight to remain within | |
| // the 8x8 chessboard | |
| bool limits(int x, int y) | |
| { | |
| return ((x >= 0 && y >= 0) && (x < N && y < N)); | |
| } | |
| /* Checks whether a square is valid and empty or not */ | |
| bool isempty(int a[], int x, int y) | |
| { | |
| return (limits(x, y)) && (a[y*N+x] < 0); | |
| } | |
| /* Returns the number of empty squares adjacent | |
| to (x, y) */ | |
| int getDegree(int a[], int x, int y) | |
| { | |
| int count = 0; | |
| for (int i = 0; i < N; ++i) | |
| if (isempty(a, (x + cx[i]), (y + cy[i]))) | |
| count++; | |
| return count; | |
| } | |
| // Picks next point using Warnsdorff's heuristic. | |
| // Returns false if it is not possible to pick | |
| // next point. | |
| bool nextMove(int a[], int *x, int *y) | |
| { | |
| int min_deg_idx = -1, c, min_deg = (N+1), nx, ny; | |
| // Try all N adjacent of (*x, *y) starting | |
| // from a random adjacent. Find the adjacent | |
| // with minimum degree. | |
| int start = rand()%N; | |
| for (int count = 0; count < N; ++count) | |
| { | |
| int i = (start + count)%N; | |
| nx = *x + cx[i]; | |
| ny = *y + cy[i]; | |
| if ((isempty(a, nx, ny)) && | |
| (c = getDegree(a, nx, ny)) < min_deg) | |
| { | |
| min_deg_idx = i; | |
| min_deg = c; | |
| } | |
| } | |
| // IF we could not find a next cell | |
| if (min_deg_idx == -1) | |
| return false; | |
| // Store coordinates of next point | |
| nx = *x + cx[min_deg_idx]; | |
| ny = *y + cy[min_deg_idx]; | |
| // Mark next move | |
| a[ny*N + nx] = a[(*y)*N + (*x)]+1; | |
| // Update next point | |
| *x = nx; | |
| *y = ny; | |
| return true; | |
| } | |
| /* displays the chessboard with all the | |
| legal knight's moves */ | |
| void print(int a[]) | |
| { | |
| for (int i = 0; i < N; ++i) | |
| { | |
| for (int j = 0; j < N; ++j) | |
| printf("%d\t",a[j*N+i]); | |
| printf("\n"); | |
| } | |
| } | |
| /* checks its neighbouring squares */ | |
| /* If the knight ends on a square that is one | |
| knight's move from the beginning square, | |
| then tour is closed */ | |
| bool neighbour(int x, int y, int xx, int yy) | |
| { | |
| for (int i = 0; i < N; ++i) | |
| if (((x+cx[i]) == xx)&&((y + cy[i]) == yy)) | |
| return true; | |
| return false; | |
| } | |
| /* Generates the legal moves using warnsdorff's | |
| heuristics. Returns false if not possible */ | |
| bool findClosedTour() | |
| { | |
| // Filling up the chessboard matrix with -1's | |
| int a[N*N]; | |
| for (int i = 0; i< N*N; ++i) | |
| a[i] = -1; | |
| // Randome initial position | |
| int sx = rand()%N; | |
| int sy = rand()%N; | |
| // Current points are same as initial points | |
| int x = sx, y = sy; | |
| a[y*N+x] = 1; // Mark first move. | |
| // Keep picking next points using | |
| // Warnsdorff's heuristic | |
| for (int i = 0; i < N*N-1; ++i) | |
| if (nextMove(a, &x, &y) == 0) | |
| return false; | |
| // Check if tour is closed (Can end | |
| // at starting point) | |
| if (!neighbour(x, y, sx, sy)) | |
| return false; | |
| print(a); | |
| return true; | |
| } | |
| // Driver code | |
| int main() | |
| { | |
| // To make sure that different random | |
| // initial positions are picked. | |
| srand(time(NULL)); | |
| // While we don't get a solution | |
| while (!findClosedTour()) | |
| { | |
| ; | |
| } | |
| return 0; | |
| } |
